





E-mail: dacomath@yahoo.com
Web: www.matematicar.in.rs
![]()

![]()
KVADRATURA KRUGA |
Kvadratura kruga je jedan od najstarijih i najpoznatijih matematičkih problema. Problem kvadrature kruga glasi: Konstruisati kvadrat |
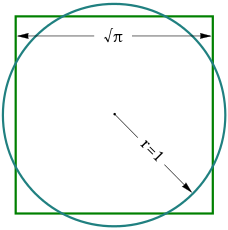 |
| Ako poluprečnik datog kruga obeležimo sa r, a stranicu traženog kvadrata sa x, dobijamo da je |
Za problem kvadrature kruga možemo reći da je star bar 2500 godina, jer je u Rajndovom papirusu izloženo pravilo za približno određivanje stranice kvadrata čija je površina jednaka površini datog kruga: Prečnik kruga treba umanjiti za devetinu i na taj način se dobije stranica traženog kvadrata. |
Prvi ozbiljniji pokušaj rešavanja ovog problema imali su Grci. Ovim problemomom bavili su se Anaksagora (5. vek p.n.e.), osnivač atinske filozofske škole, kao i Antifon iz Atine (5. vek p.n.e.) koji je izračunao površinu kruga tako što je upisivao u njega sve veće pravilne n-touglove. |
 |
Arhimed (3. vek p.n.e.), je koristeći upisane i opisane mnogouglove dokazao da je obim kruga tri puta veći od prečnika, i još nešto više, tacnije za manje od sedmine, ali za više od deset sedamdesetjednina. Tim postupkom Arhimed dolazi do vrednosti: |
Leonardo da Vinči je pokušao da problem kvadrature kruga reši mehaničkim putem tako što je konstruisao pravi valjak čija je visina bila jednaka četvrtini prečnika njegove osnove. Arapski matematičar Al Kaši (14. vek) izračunao je dosta preciznije broj Međutim svi njegovi pokušaji, kao i mnogih drugih matematičara ostali su bez rezultata. |
 |
Tek u 19. veku, tačnije 1882. godine nemački matematičar Lindman će pokazati da je broj Problem kvadrature kruga se praktično i svodio na konstrukciju broja |